Particle Swarm Optimization¶
This solver is implemented in optunity.solvers.ParticleSwarm. It as available in optunity.make_solver() as ‘particle swarm’.
Particle swarm optimization (PSO) is a heuristic optimization technique. It simulates a set of particles (candidate solutions) that are moving aroud in the search-space [PSO2010], [PSO2002].
In the context of hyperparameter search, the position of a particle represents a set of hyperparameters and its movement is influenced by the goodness of the objective function value.
PSO is an iterative algorithm:
Initialization: a set of particles is initialized with random positions and initial velocities. The initialization step is essentially equivalent to Random Search.
Iteration: every particle’s position is updated based on its velocity, the particle’s historically best position and the entire swarm’s historical optimum.
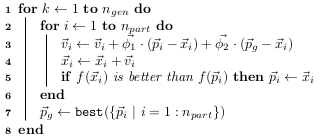
Particle swarm iterations:
- \(\vec{x}_i\) is a particle’s position,
- \(\vec{v}_i\) its velocity,
- \(\vec{p}_i\) its historically best position,
- \(\vec{p}_g\) is the swarm’s optimum,
- \(\vec{\phi}_1\) and \(\vec{\phi}_2\) are vectors of uniformly sampled values in \((0, \phi_1)\) and \((0, \phi_2)\), respectively.
PSO has 5 parameters that can be configured (see optunity.solvers.ParticleSwarm):
- num_particles: the number of particles to use
- num_generations: the number of generations (iterations)
- phi1: the impact of each particle’s historical best on its movement
- phi2: the impact of the swarm’s optimum on the movement of each particle
- max_speed: an upper bound for \(\vec{v}_i\)
The number of function evaluations that will be performed is num_particles * num_generations. A high number of particles focuses on global, undirected search (just like Random Search), whereas a high number of generations leads to more localized search since all particles will have time to converge.
Bibliographic references:
| [PSO2010] | Kennedy, James. Particle swarm optimization. Encyclopedia of Machine Learning. Springer US, 2010. 760-766. |
| [PSO2002] | Clerc, Maurice, and James Kennedy. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. Evolutionary Computation, IEEE Transactions on 6.1 (2002): 58-73. |